Rapid EM Modelling
Published:
Rapid Electromagnetics modelling for mobile platforms
In order to understand the performance envelope of a complex system like an antenna array, some method of exploring the problem space is required. If this method is to be useful it must deliver results with if not perfect, are at least accurate enough to inform reliable judgments, such as where to allocate development funds for say more detailed, and accurate models, and eventually prototypes. If a proposed antenna array design is available, then there are a number of electromagnetics packages such as HFSS and CST which will allow the user to produce accurate prediction of the designs performance, These types of packages come with two drawback, in order to evaluate the performance on the platform in question the array design must be complete enough to be simulated in this way, and the computational resources required to mesh the entire platform may well be significant in terms of both time investment and expense.

A UAV such as shown here may well represent the easiest example, because it may well be small enough to allow on platform models. But even at this scale, and say S or X band, the computational complexity to model such a platform is not trivial.
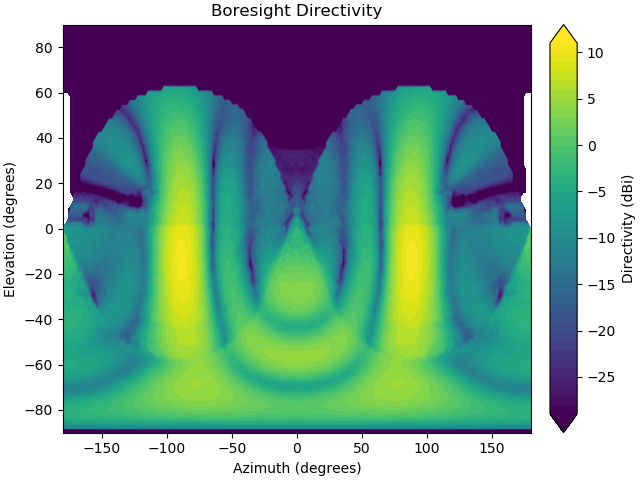
However, a useful way to model this problem is to start with just the structure and a desired array size and position. In this example the proposed array is to be mounted on the lower nose, and a frequency of 6GHz is selected. By combining some raycasting with electromagnetics, and modelling the array as a surface of z directed electric current sources the farfield pattern of the resultant array can be conveniently predicted.

In this way the Etheta, and Ephi patterns can be viewed and evaluated. 
Indeed the resultant total directivity pattern can also be calculated. However, this method is presented here without beamforming so it does not yet provide the "True" performance envelope in terms of say maximum achievable gain and steering efficiency. But this is an implementation problem, and one that is easily rectified.