Modelling Microwave Power Transfer
Published:
A critical part of the development of LyceanEM in support of the development of Space-based Solar Power is the development of a robust and accurate model for microwave propagation. The critical issue for space-based solar power is an accurate prediction of the losses from propagation through the different layers of the atmosphere for extremely large scale microwave beams, over 1km in radius. This level of electromagnetics modelling is beyond the capability of current commercial software, and requires the development of new open-source tools to support the development of the technology.
Scalable Open Electromagnetics for Solar Power (SCOPES)
The SCOPES project is a collaboration between the University of Bristol and Virtus Solis, funded by the Department for Net Zero and Energy Security. The project aims to develop the computational tools required to design and operate the gigascale antenna arrays required for Space-based Solar Power, based around the development of LyceanEM.
One of the primary challenges for the development of LyceanEM is moving from a farfield model of radio propagation, to a more comprehensive propagation algorithm. LyceanEM was based upon the use of ray-like propagation assumptions of Physical Optics and the Huygens-Fresnel principle. This is a good approximation for the farfield, but is somewhat lacking both for the consideration of lossy mediums such as the atmosphere, and for the nearfield regime required for efficient power transfer at scale.
Fraunhofer-(Farfield)
\[U_{p^{'}(r)}=\dfrac{\lambda}{4\pi}\int\int_AU(p)\dfrac{e^{j\beta r}}{r}\]In order to include a more rigorous model of microwave propagation, the use of the Rayleigh-Sommerfeld diffraction integral was considered as the more general form, modelling the propagation of electromagnetic waves in the nearfield. This model is also based upon the Huygens-Fresnel principle, and is a more general form of the Fraunhofer model, which is valid for the nearfield as well as the farfield. However, this integral is based upon the modelling of aperture and image planes, and is not well suited to the modelling of antenna arrays of arbitrary geometries, nor does it consider the effects of polarization. Importantly for efficient computation of omnidirectional antenna arrays such as CASSIOPeiA, it also imposes a cosine dependence on the angle of propagation for each ray component, which implies that an omnidirectional antenna can only be modelled using a sufficient number of sources to approximate the omnidirectional radiation pattern. This approximation is well considered for optical frequencies when considering paraxial propagation between two parallel planes, but is less well suited to microwave and radio fequencies.
\[U_{p^{'}(r)}=\dfrac{1}{i\lambda}\int\int_A U(p)\cos(\vec{n_{p}},\vec{r})\dfrac{e^{ikr}}{r}dxdy\]The arbitrary propagation integral derived for LyceanEM is a derivation of the Rayleigh-Sommerfeld diffraction integral, generalized to arbitary geometries, and explicitly including the consideration of lossy media (propagation constant $\gamma=\alpha+i\beta$) and polarized wave propagation via the field transform based upon the angle of propagation from the source ($A_{p}$).
Arbitrary Propagation Integral
\[U_{p^{'}(r)}=-\dfrac{1}{2\pi}\int\int_\sum U(p)A_{p}(\alpha+i\beta)\cos(\vec{n_{p^{'}}},\vec{r})\dfrac{e^{-(\alpha +i\beta)r+\psi}}{r}ds\]Algorithm Comparison
A useful introduction to the challenge of modelling wireless power transfer can be found in Computation of Power Beaming Efficiency in the Fresnel Zone with Application to Amplitude and Phase Optimization which was drawn up at the Naval Research Laboratory by Judith Hutson. This report introduces a Matlab based propagation tool using a version of the Rayleigh-Sommerfled algorithm to predict the received fields from a transmitting array, and introduces useful concepts for the specification of calibrated power on a discrete transmitting aperture. The included figure shows a comparison of the proposed algorithm with the Fraunhofer approximation (Simple in blue), a CPU isotropic implementation of the arbitary propagation integral, and two difference beamforming weights used with the arbitary propagation integral as implemented within the latest version of LyceanEM (0.0.7). The two beamforming approches are Equiphase, for which the transmitting element phases are calculated to provide an equiphase surface centered at the focal point of the receiving array, and Kaiser which uses a Kaiser windowing function to calculate amplitude weights to provide a more focused beam. The comparison is made for two 4sqm apertures at 10GHz and a transmit power of 100W, with the range between these two parallel apertures varying from 0.1m to over 1000m. The Theoretical Max included is based upon the derived upper bound by Goubau for the maximum power transfer efficiency $\eta$ between two parallel apertures $A_{t}$ and $A{r}$ at distance $D$ [1].
Theoretical Maximum Transfer Efficiency
\[\tau=\dfrac{\sqrt(A_{t}A_{r})}{\lambda D}\]$\tau$ allowing the maximum possible transfer efficiency $\eta$ to be calculated.
\[\eta=1-e^{\tau^{2}}\]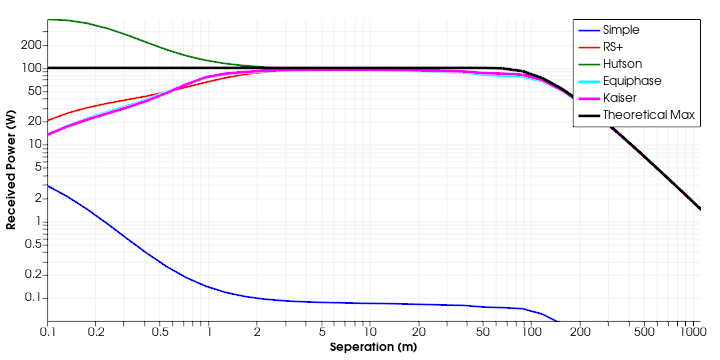
Visualising Large Scale Power Transfer - International Conference on Energy from Space
At the International Conference on Energy from Space in April 2024 I delivered a talk on SCOPES. We demonstrated a “small scale” model of wireless power transfer, from a circular transmitting array with a diameter of 34m and 250,000 antenna elements, over a distance of 5.9km, to an elliptical receiving antenna array with maximum diameter of 37m, and 1 million antenna elements. Based upon a target power density of 240W/m2, this small scale setup would be able to transfer 253kW. While the receiving station was sited just outside Walton in Gordano, the transmitting antenna array was arranged so that it would replicate the illumination angle of a geosynchronus satellite. While the scale of computation required for a full scale 2GW demonstration is still an ambitious goal, the demonstration showed the potential of LyceanEM to scale up to the required level with sufficient computational resources. The focus for the future is on the development of increasingly efficient computational approaches to support full scale modelling within convenient timescales, allowing the investigation of novel beamforming approaches to manage the power transfer efficiently and safely. This talk included a visualisation of the illuminated power from the transmitting power station, and a comparison of Space-Based Solar Power Concepts.
[1] Qiang Chen, Xing Chen & Xin Duan. (2018) Investigation on beam collection efficiency in microwave wireless power transmission. Journal of Electromagnetic Waves and Applications 32:9, pages 1136-1151.
